ĐỊNH NGHĨA, ĐỊNH LÝ VỀ TAM THỨC BẬC 2

Trung tâm luyện thi, gia sư - dạy kèm tại nhà NTIC Đà Nẵng giới thiệu phần ĐỊNH NGHĨA, ĐỊNH LÝ VỀ TAM THỨC BẬC 2. nhằm hổ trợ cho các bạn có thêm tư liệu học tập. Chúc các bạn học tốt môn học này.

Ngày đăng: 12-03-2018

2,042 lượt xem

1. Định nghĩa

- Tam thức bậc hai (một ẩn) là đa thức có dạng $f (x) = a x^{2} + b x + c$ $f (x) = a x^{2} + b x + c$ trong đó $x$ $x$ là biến $a, b, c$ $a, b, c$ là các số đã cho, với $a \neq 0$

2. Định lí

$f (x) = a x^{2} + b x + c (a \neq 0)$ $f (x) = a x^{2} + b x + c (a \neq 0)$ có biệt thức $∆ = b^{2} - 4 a c$ $∆ = b^{2} - 4 a c$ .

- Nếu $∆ < 0$ $∆ < 0$ thì với mọi $x, f (x)$ $x, f (x)$ có cùng dấu với hệ số $a$ $a$ .

- Nếu $∆ = 0$ $∆ = 0$ thì $f (x)$ $f (x)$ có nghiệm kép $x = - \frac{b}{2 a}$ $x = - \frac{b}{2 a}$ , với mọi $x \neq - \frac{b}{2 a}$ $x \neq - \frac{b}{2 a}$ , $f (x)$ $f (x)$ có cùng dấu với hệ số $a$ $a$ .

- Nếu $∆ > 0, f (x)$ $∆ > 0, f (x)$ có $2$ $2$ nghiệm $x_{1}, x_{2} (x_{1} < x_{2})$ $x_{1}, x_{2} (x_{1} < x_{2})$ và luôn cùng dấu với hệ số $a$ $a$ với mọi $x$ $x$ ngoài đoạn $[x_{1}; x_{2}]$ $[x_{1}; x_{2}]$ và luôn trái dấu với hệ số $a$ $a$ với mọi $x$ $x$ trong đoạn $(x_{1}; x_{2})$

$(x_{1}; x_{2})$

Bài 1. Xét dấu các tam thức bậc hai

a) $x^{2} - 3 x + 1$ $x^{2} - 3 x + 1$ ;

b) $- 2 x^{2} + 3 x + 5$ $- 2 x^{2} + 3 x + 5$ ;

c) $x^{2} + 12 x + 36$ $x^{2} + 12 x + 36$ ;

d) $(2 x - 3) (x + 5)$ $(2 x - 3) (x + 5)$ .

Giải

a) $x^{2} - 3 x + 1$ $x^{2} - 3 x + 1$

$∆ = (- 3)^{2} - 4.5 < 0 \Rightarrow 5 x^{2} - 3 x + 1 > 0, \forall x \in R$ $∆ = (- 3)^{2} - 4.5 < 0 \Rightarrow 5 x^{2} - 3 x + 1 > 0, \forall x \in R$ (vì luôn cùng dấu với $a = 5 > 0$ $a = 5 > 0$ ).

b) $- 2 x^{2} + 3 x + 5$ $- 2 x^{2} + 3 x + 5$

$- 2 x^{2} + 3 x + 5 = 0 \Leftrightarrow [\begin{matrix} x = - 1 \\ x = \frac{5}{2} \end{matrix}$ $- 2 x^{2} + 3 x + 5 = 0 \Leftrightarrow [\begin{matrix} x = - 1 \\ x = \frac{5}{2} \end{matrix}$

$- 2 x^{2} + 3 x + 5 < 0$ $- 2 x^{2} + 3 x + 5 < 0$ với $x \notin [- 1; \frac{5}{2}]$ $x \notin [- 1; \frac{5}{2}]$

$- 2 x^{2} + 3 x + 5 > 0$ $- 2 x^{2} + 3 x + 5 > 0$ với $- 1 < x < \frac{5}{2}$ $- 1 < x < \frac{5}{2}$ .

c) $x^{2} + 12 x + 36$ $x^{2} + 12 x + 36$

$Δ^{'} = 6^{2} - 1.36 = 0$ $Δ^{'} = 6^{2} - 1.36 = 0$

$x^{2} + 12 x + 36 = 0 \Leftrightarrow x = - 6$ $x^{2} + 12 x + 36 = 0 \Leftrightarrow x = - 6$

Do đó: $x^{2} + 12 x + 36 > 0, \forall x \neq - 6$ $x^{2} + 12 x + 36 > 0, \forall x \neq - 6$ .

d) $(2 x - 3) (x + 5) = 2 x^{2} + 7 x - 15$ $(2 x - 3) (x + 5) = 2 x^{2} + 7 x - 15$

$(2 x - 3) (x + 5) = 0 \Leftrightarrow [\begin{matrix} x = - 5 \\ x = \frac{3}{2} \end{matrix}$ $(2 x - 3) (x + 5) = 0 \Leftrightarrow [\begin{matrix} x = - 5 \\ x = \frac{3}{2} \end{matrix}$

Hệ số của tam thức là: $a = 2 > 0$ $a = 2 > 0$ . Do đó:

$(2 x - 3) (x + 5) > 0$ $(2 x - 3) (x + 5) > 0$ với $x \notin [- 5; \frac{3}{2}]$ $x \notin [- 5; \frac{3}{2}]$

$(2 x - 3) (x + 5) < 0$ $(2 x - 3) (x + 5) < 0$ với $x \notin (- 5; \frac{3}{2}) .$

$x \notin (- 5; \frac{3}{2}) .$

a) $f (x) = (3 x^{2} - 10 x + 3) (4 x - 5)$ $f (x) = (3 x^{2} - 10 x + 3) (4 x - 5)$ ;

b) $f (x) = (3 x^{2} - 4 x) (2 x^{2} - x - 1)$ $f (x) = (3 x^{2} - 4 x) (2 x^{2} - x - 1)$ ;

c) $f (x) = (4 x^{2} - 1) (- 8 x^{2} + x - 3) (2 x + 9)$ $f (x) = (4 x^{2} - 1) (- 8 x^{2} + x - 3) (2 x + 9)$ ;

d) $f (x) = \frac{(3 x^{2} - x) (3 - x^{2})}{4 x^{2} + x - 3} .$ $f (x) = \frac{(3 x^{2} - x) (3 - x^{2})}{4 x^{2} + x - 3} .$

Giải

a) $f (x) = (3 x^{2} - 10 x + 3) (4 x - 5)$ $f (x) = (3 x^{2} - 10 x + 3) (4 x - 5)$

$3 x^{2} - 10 x + 3 = 0 \Leftrightarrow [\begin{matrix} x = \frac{1}{3} \\ x = 3 \end{matrix}$ $3 x^{2} - 10 x + 3 = 0 \Leftrightarrow [\begin{matrix} x = \frac{1}{3} \\ x = 3 \end{matrix}$

$4 x - 5 = 0 \Leftrightarrow x = \frac{5}{4}$ $4 x - 5 = 0 \Leftrightarrow x = \frac{5}{4}$

Bảng xét dấu:

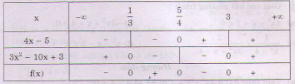
Kết luận:

$f (x) < 0$ $f (x) < 0$ với $x \in (- \infty; \frac{1}{3}) \cup (\frac{5}{4}; 3)$ $x \in (- \infty; \frac{1}{3}) \cup (\frac{5}{4}; 3)$

$f (x) > 0$ $f (x) > 0$ với $x \in (\frac{1}{3}; \frac{5}{4}) \cup (3; + \infty)$

$x \in (\frac{1}{3}; \frac{5}{4}) \cup (3; + \infty)$

b) $f (x) = (3 x^{2} - 4 x) (2 x^{2} - x - 1) = 0$ $f (x) = (3 x^{2} - 4 x) (2 x^{2} - x - 1) = 0$

$\Leftrightarrow [\begin{matrix} x = 0 \\ x = \frac{4}{3} \\ x = 1 \\ x = - \frac{1}{2} \end{matrix}$ $\Leftrightarrow [\begin{matrix} x = 0 \\ x = \frac{4}{3} \\ x = 1 \\ x = - \frac{1}{2} \end{matrix}$

Bảng xét dấu:

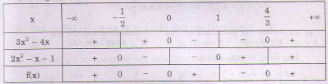
c) $f (x) = (4 x^{2} - 1) (- 8 x^{2} + x - 3) (2 x + 9) = 0$ $f (x) = (4 x^{2} - 1) (- 8 x^{2} + x - 3) (2 x + 9) = 0$

$\Leftrightarrow [\begin{matrix} x = \frac{1}{2} \\ x = - \frac{1}{2} \\ x = - \frac{9}{2} \end{matrix}$ $\Leftrightarrow [\begin{matrix} x = \frac{1}{2} \\ x = - \frac{1}{2} \\ x = - \frac{9}{2} \end{matrix}$

Bảng xét dấu:

d) $f (x) = \frac{(3 x^{2} - x) (3 - x^{2})}{4 x^{2} + x - 3} .$ $f (x) = \frac{(3 x^{2} - x) (3 - x^{2})}{4 x^{2} + x - 3} .$
$f (x) = \frac{(3 x^{2} - x) (3 - x^{2})}{4 x^{2} + x - 3} = 0$

$\Leftrightarrow [\begin{matrix} x = \sqrt{3} \\ x = - \sqrt{3} \\ x = \frac{1}{3} \\ x = 0 \end{matrix}$ $\Leftrightarrow [\begin{matrix} x = \sqrt{3} \\ x = - \sqrt{3} \\ x = \frac{1}{3} \\ x = 0 \end{matrix}$

Bảng xét dấu:

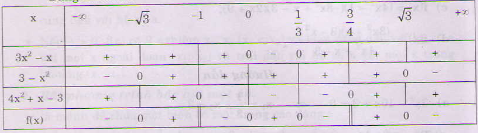
Bài 3. Giải các bất phương trình sau

a) $4 x^{2} - x + 1 < 0$ $4 x^{2} - x + 1 < 0$ ;

b) $- 3 x^{2} + x + 4 \geq 0$ $- 3 x^{2} + x + 4 \geq 0$ ;

giải

a) Tam thức $f (x) = 4 x^{2} - x + 1 < 0$ $f (x) = 4 x^{2} - x + 1 < 0$ có hệ số $a = 4 > 0$ $a = 4 > 0$ biệt thức $∆ = (- 1)^{2} - 4.4.1 < 0$ $∆ = (- 1)^{2} - 4.4.1 < 0$ . Do đó $f (x) > 0, \forall x \in R$ $f (x) > 0, \forall x \in R$ .

Bất phương trình $4 x^{2} - x + 1 < 0$ $4 x^{2} - x + 1 < 0$ vô nghiệm.

b) $- 3 x^{2} + x + 4 \geq 0$ $- 3 x^{2} + x + 4 \geq 0$

$f (x) = - 3 x^{2} + x + 4 = 0 \Leftrightarrow [\begin{matrix} x = - 1 \\ x = \frac{4}{3} \end{matrix}$ $f (x) = - 3 x^{2} + x + 4 = 0 \Leftrightarrow [\begin{matrix} x = - 1 \\ x = \frac{4}{3} \end{matrix}$

Do đó: $- 3 x^{2} + x + 4 \geq 0 \Leftrightarrow - 1 \leq x \leq \frac{4}{3}$ $- 3 x^{2} + x + 4 \geq 0 \Leftrightarrow - 1 \leq x \leq \frac{4}{3}$

Bài 4. Tìm các giá trị của tham số $m$ $m$ để các phương trình sau vô nghiệm

a) $(m - 2) x^{2} + 2 (2 m - 3) x + 5 m - 6 = 0$ $(m - 2) x^{2} + 2 (2 m - 3) x + 5 m - 6 = 0$ ;

b) $(3 - m) x^{2} - 2 (m + 3) x + m + 2 = 0$ $(3 - m) x^{2} - 2 (m + 3) x + m + 2 = 0$ .

Giải

a) +) Với $m = 2$ $m = 2$ phương trình trở thành $2 x + 4 = 0$ $2 x + 4 = 0$ có $1$ $1$ nghiệm, do đó trường hợp này không thỏa mãn.

+) Với $m \neq 2$ $m \neq 2$

Phương trình vô nghiệm nếu:

${\begin{matrix} m - 2 \neq 0 \\ Δ^{^{'}} = (2 m - 3)^{2} - (m - 2) (5 m - 6) < 0 \end{matrix}$ ${\begin{matrix} m - 2 \neq 0 \\ Δ^{^{'}} = (2 m - 3)^{2} - (m - 2) (5 m - 6) < 0 \end{matrix}$

$\Leftrightarrow$ $\Leftrightarrow$ ${\begin{matrix} m - 2 \neq 0 \\ - m^{2} + 4 m - 3 < 0 \end{matrix}$ ${\begin{matrix} m - 2 \neq 0 \\ - m^{2} + 4 m - 3 < 0 \end{matrix}$

$\Leftrightarrow m < 1 \cup m > 3$ $\Leftrightarrow m < 1 \cup m > 3$ .

b) +) Với $m = 3$ $m = 3$ , phương trình trở thành: $- 6 x + 5 = 0$ $- 6 x + 5 = 0$ có nghiệm. Loại trường hợp $m = 3$ $m = 3$ .

+) Với $m \neq 3$ $m \neq 3$

Phương trình vô nghiệm khi và chỉ khi:

$\begin{aligned} \Leftrightarrow {\begin{matrix} m \neq 3 \\ Δ^{'} = (m + 3)^{2} - (3 - m) . (m + 2) < 0 \end{matrix} \\ \Leftrightarrow {\begin{matrix} m \neq 3 \\ 2 m^{2} + 5 m + 3 < 0 \end{matrix} \Leftrightarrow - \frac{3}{2} < m < - 1 \end{aligned}$