KHÁI NIỆM, ĐỒ THỊ VỀ HÀM SỐ, HÀM SỐ ĐỒNG BIẾN VÀ HÀM SỐ NGHỊCH BIẾN

1. Khái niệm hàm số

 - Cho X, Y là hai tập hợp số, ví dụ tập số thực R, hàm số f xác định trên X, nhận giá trị trong Y là một quy tắc cho tương ứng mỗi số x thuộc X với một số y duy nhất thuộc Y.

Ký hiệu

${\displaystyle f\colon X\to Y}$$$$$$$ hoặc $${\displaystyle f\colon x\mapsto f(x)} hoặc

${\displaystyle y=f(x)\,\!}$$$$$$$

Với:

• Tập X gọi là miền xác định.
• Tập Y gọi là miền giá trị.
• x gọi là biến độc lập hay còn gọi là đối số.
• y gọi là biến phụ thuộc hay còn được gọi là hàm số.
• f(x) được gọi là giá trị của hàm f tại x.

 

2. Hàm số được cho bằng hai dạng : bảng và công thức.

a. Hàm số dạng bảng 

 

x	0	1	2	3	4	5
y	1	3	5	7	9	11

 

b. Hàm số bằng công thức (dạng tường minh):

y = f(x)

f(x) là biểu thức đại số với biến x.

Ví dụ :

y = 2 : hàm hằng.

y = 2x +1: hàm số bậc nhất

y = x² +2x -1: hàm số bậc 2

  hàm số nhất biến .v .v …

 

3. Tập giá trị và tập xác định :

Tập giá trị Y là tập hợp các giá trị của hàm số y.

Tập xác định X tập hợp các giá trị của biến số x. Tập xác định X của hàm số y xác định.

 

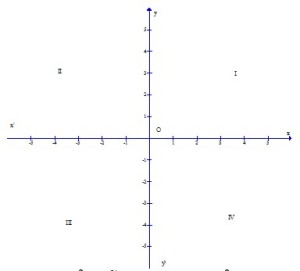
4. Đồ thị của hàm số 

a. Định nghĩa

Đồ thị của hàm số y = f(x) là tập hợp các cặp giá trị tương ứng (x ; f(x)) trên mặt phẳng tọa độ.

 

b. mặt phẳng tọa độ Oxy 

 * Ox :trục hoành.

* Oy : trục tung.

* O : gốc tọa độ.

* ( I) góc phần tư thứ I, (II) góc phần tư thứ iI,( III) góc phần tư thứ III,( IV) góc phần tư thứ IV.

 

c. Biểu diễn tọa độ một điểm A trên mặt phẳng tọa độ Oxy:

Ta có : A(x_A ; y_A) trong đó :     x_A: hoành độ của điểm A .

y_A: hoành độ của điểm A .

ví dụ Biểu diễn tọa độ một điểm A(2 ; 3)

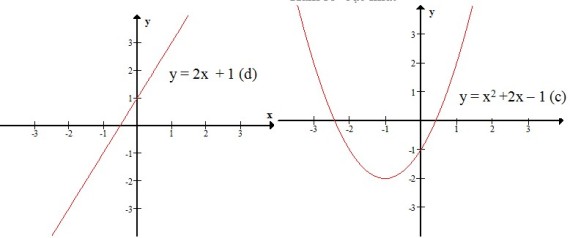
vẽ đồ thị của một hàm số trên mặt phẳng tọa độ:

y = x² +2x – 1 (c); y = 2x + 1 (d)

5. Vị trí tương đối giữa điểm và đồ thị hàm số :

cho A(x_A ; y_A) và hàm số y = f(x) có đồ thị (c). A thuộc (c) khi y_A = f(x_A)

ví dụ : A(1 ; 2) và B( -2 ; 1) có thuộc y = f(x) = x² +2x – 1 (c)

giải.

Tính : f(x_A) = f(1) = 1² +2.1 – 1 = 2 = y_A

=> A € ( c).

f(x_B) = f(-2) = (-2)² +2.(-2) – 1 = 2 = -1 ≠ y_B

=> B không nằm trên (C).

 

6. Hàm số đồng biến và hàm số nghịch biến 

a. Định nghĩa 

Cho hàm số y = f(x) xác định với mọi giá trị của x thuộc R.

• Nếu giá trị của biến tăng lên mà giá trị tương ứng của hàm số f(x) cũng tăng lên
  thì hàm số y = f(x) được gọi là hàm số đồng biến trên R (gọi tắt là hàm số đồng biến).
• Nếu giá trị của biến tăng lên mà giá trị tương ứng của hàm số f(x) cũng giảm đi
  thì hàm số y = f(x) được gọi là hàm số nghịch biến trên R (gọi tắt là hàm số nghịch biến).

 

b. Định lí : với x₁, x₂ thuộc R.

• Nếu x₁ < x₂ mà f(x₁) < f(x₂) thì hàm số y = f(x) đồng biến trên R.
• Nếu x₁ < x₂ mà f(x₁) > f(x₂) thì hàm số y = f(x) nghịch biến trên R.

Ví dụ :hàm số sau đồng biến hay nghịch biến : y = f(x) = -2x +1

Giải

Tập xác định : R

với x₁, x₂ thuộc R sao cho x₁ < x₂ = > x₂ – x₁ > 0 (1)

tính : f(x₁) = -2x₁ +1;  f(x₂) = -2x₂ +1

xét : f(x₁) – f(x₂) = (-2x₁ +1) – (-2x₂ +1) = -2x₁ +1 +2x₂ -1 = 2(x₂ – x₁) >0 (vì x₂ – x₁ > 0 )

=> f(x₁) > f(x₂) vậy : hàm số nghịch biến.

BÀI TẬP SGK

BÀI 1 TRANG 44:

Cho hàm số y = f(x) = 

tính :  f(-2) = 

f(0) = 

 

BÀI 7 TRANG 46:

Cho hàm số y = f(x) = 3x . Cho hai số x₁, x₂ thuộc R sao cho x₁ < x₂

Hãy chứng minh  f(x₁) < f(x₂) rồi rút ra kết luận hàm số đồng biến trên R

Giải

Tập xác định : R

Cho hai số x₁, x₂ thuộc R sao cho x₁ < x₂= > x₂ – x₁ > 0

tính : f(x₁) = 3x₁ +1;  f(x₂) =3x₂ +1

xét : f(x₂) – f(x₁) = 3x₂ – 3x₁  = 3(x₂ – x₁) >0 (vì x₂ – x₁ > 0 )

=> f(x₁) <  f(x₂) vậy : hàm số đồng biến trên R .

BÀI TẬP BỔ SUNG :

 Tính giá trị của hàm số tại x = x₀ :

Cho hàm số y = f(x).

Bước 1.   Thế giá trị của biến x bằng x₀. (chổ nào có x thế bằng x₀).

Bước 2.    Tính y₀ = f(x₀).

 =================================

Ví dụ minh họa : cho hàm số y = f(x) = x³ + 2x² -3x -1 tại x = 2.

Giài.

Y₀ = f(2) =  2³ + 2.2² -3.2 -1 ( bước 1).

= 9 (bước 2)

vậy : y₀ = 9

Trung tâm luyện thi, gia sư - dạy kèm tại nhà NTIC Đà Nẵng