TÓM TẮT LÍ THUYẾT VÀ GIẢI BÀI TẬP GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT CUNG

I. TÓM TẮT LÍ THUYẾT

1. Định nghĩa

Trên đường tròn lượng giác cho cung  có số đo sđ  = α thì:

+ Tung độ của M gọi là sin của α, kí hiệu sinα:  = sinα

+ Hoành độ của M gọi là cosin của α, kí hiệu là cosα:  = cosα

+ Nếu cosα # 0, ta gọi là tang của α, kí hiệu tanα là tỉ số:  = tanα

+ Nếu sinα # 0, ta gọi là cotang của α, kí hiệu là  = cotα

Ghi chú: Vì sđ  = sđ (OA, OM) nên định nghĩa các giá trị lượng giác của cung lượng giác α cũng là giá trị lượng giác của góc lượng giác α.

2. Hệ quả

a) -1 ≤ sinα ≤ 1, -1 ≤ cosα ≤ 1 ∀α thuộc R 

sin(α + k2π) = sinα ∀k thuộc Z

cos(α + k2π) = cosα ∀k thuộc Z

b) tanα xác định với mọi α #  + kπ, ∀k thuộc Z

cotα xác định với mọi α # kπ, ∀k thuộc Z

                tan(α + kπ) = tanα ∀k thuộc Z

                cot(α + kπ) = cotα ∀k thuộc Z

c) Bảng xác định dấu của các giá trị lượng giác

 

d) Các hệ thức lượng giác cơ bản:

sin²α + cos²α = 1;                 tanα.cotα = 1

1 + tan²α =                  1 + cot²α = 

3. Giá trị lượng giác của các cung có liên quan đặc biệt

a) Cung đối nhau: α và (-α)

sin(-α) = -sinα                      tan(-α) = -tanα

cos(-α) = cosα                       cot(-α) = -cotα

 

b) Cung bù nhau: α và π – α

sin(π – α) = sinα                              tan(π – α) = -tanα

cos(π – α) = -cosα                            cot(π – α) = -cotα

 

c) Cung hơn nhau π: α và π + α 

sin(π + α) = -sinα                   tan(π + α) = tanα

cos(π + α) = -cosα                 cot(π + α) = cotα

 

d) Cung phụ nhau: α và (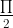 – α)

sin( – α) = cosα                                tan( – α) = cosα

cos( – α) = sinα                                cot( – α) = tanα

II. BÀI TẬP VẬN DỤNG

Bài 1 trang 148 sgk đại số 10

Bài 1. Có cung α nào mà sinα nhận các giá trị tương ứng sau đây không?  

a) -0,7;    b)      c) -√2;          d) 

Hướng dẫn giải:

a) -1 ≤ -0,7 ≤ 1. Có cung α mà sin α = -0,7

b)  > 1. Không có cung α có sin nhận giá trị 

c) Không. Vì -√2 < -1

d) Không. Vì  > 1

Bài 2 trang 148 sgk đại số 10

Bài 2. Các đẳng thức sau có thể đồng thời xảy ra không?

a) sinα =  và cosα = ;

b) sinα = – và cosα = 

Hướng dẫn giải:

a) Không. Bởi vì   < 1

b) Có thể đồng thời xảy ra, vì  = 1

c) Không. Lí do như câu a

Bài 3 trang 148 sgk đại số 10

Bài 3. Cho 0 < α < . Xác định dấu của các giá trị lượng giác

a) sin(α – π);                 b) cos( – α)

c) tan(α + π);                d) cot(α + )

Hướng dẫn giải:

Với 0 < α < :

a) sin(α – π) < 0;              b) cos( – α) < 0;

c) tan(α + π) > 0;             d) cot(α + ) < 0

Bài 4 trang 148 sgk đại số 10

Bài 4. Tính các giá trị lượng giác của góc α, nếu:

a) cosα =  và 0 < α < ;             b) sinα = -0,7 và π < α < ;

c) tan α =  và  < α < π;          d) cotα = -3 và  < α < 2π.

Hướng dẫn giải:

a) Do 0 < α <  nên sinα > 0, tanα > 0, cotα > 0

sinα = 

cotα = ; tanα = 

b) π < α <  nên sinα < 0, cosα < 0, tanα > 0, cotα > 0

cosα = -√(1 – sin² α) = -√(1 – 0,49) = -√0,51 ≈ -0,7141

 tanα ≈ 0,9802; cotα ≈ 1,0202.

c)  < α < π nên sinα > 0, cosα < 0, tanα < 0, cotα < 0 

cosα =  ≈ -0,4229.

 sinα = 

cotα = –

d) Vì  < α < 2π nên sinα < 0, cosα > 0, tanα < 0, cotα < 0

Ta có: tanα = 

 cosα = 

Bài 5 trang 148 sgk đại số 10

Bài 5. Tính α, biết:

a) cosα = 1;              b) cosα = -1

c) cosα = 0;               d) sinα = 1

e) sinα = -1;              f) sinα = 0,

Hướng dẫn giải:

a) α = k2π, k thuộc Z                                       

b) α = (2k + 1)π, k thuộc  Z

c) α =  + kπ, k thuộc  Z 

d) α =  + k2π, k thuộc  Z

e) α =  + k2π, k thuộc  Z

f) α = kπ, k thuộc  Z  

Trung tâm gia sư - dạy kèm tại nhà NTIC

(nguồn từ internet)