GIẢI PHƯƠNG TRÌNH CHỨA CĂN BẬC 2
Trung tâm luyện thi, gia sư - dạy kèm tại nhà NTIC Đà Nẵng giới thiệu phần GIẢI PHƯƠNG TRÌNH CHỨA CĂN BẬC 2 nhằm hổ trợ cho các bạn có thêm tư liệu học tập. Chúc các bạn học tốt môn học này.
Ngày đăng: 23-10-2018
8,408 lượt xem
A. Định nghĩa :
y = Đk : A ≥ 0.
B. Dạng phương trình chứa căn bậc hai cơ bản : ( k ≥ 0)
Phương pháp giải :
Bước 1 : Điều kiện : A ≥ 0
Bước 2 : ⇔ A = k2 ( k ≥ 0)
Ví dụ : giải phương trình chứa căn bậc hai
(1)
Đk : x+1 ≥ 0 ⇔ x ≥ -1
(1) ⇔
⇔
⇔ x + 1 = 4
⇔x = 3
so đk : x = 3 ≥ -1 (nhận)
vậy : S = {3}
c. Dạng phương trình chứa căn bậc hai cơ bản :
Phương pháp giải :
Bước 1 : Điều kiện : A ≥ 0
Bước 2 : bình phương : => A = B2
Bước 3 : thử nghiệm.
Ví dụ : giải phương trình chứa căn bậc hai
(3)
Đk : x – 7 ≥ 0 ⇔ x ≥ 7
(3) ⇔
=> x – 7 = (2x – 15)2
⇔ x – 7 = 4x2 – 60x + 225
⇔ 4x2 – 61x + 232 = 0
⇔ x = 8 ; x = 29/4
so đk : x = 8 ≥ 7 (đúng); và đúng
=> x = 8 (nhận)
x = 29/4 ≥ 7 (đúng) ; và (sai)
x = 29/4 (loại)
vậy : S = {8}
BÀI TẬP TỰ LUYỆN
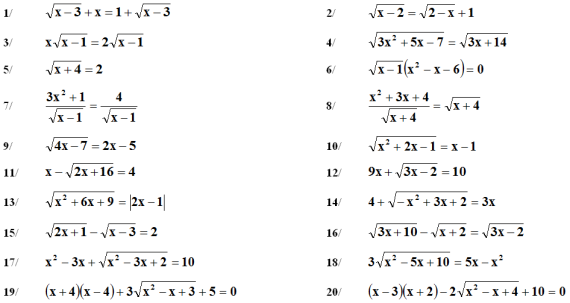
LIÊN HỆ NGAY VỚI CHÚNG TÔI ĐỂ BIẾT THÊM THÔNG TIN CHI TIẾT
ĐÀO TẠO NTIC
Địa chỉ: Đường nguyễn lương bằng, P.Hoà Khánh Bắc, Q.Liêu Chiểu, Tp.Đà Nẵng
Hotline: 0905540067 - 0778494857
Email: daotaontic@gmail.com
Tin liên quan
- › BÀI TẬP VẬN DỤNG CAO TOÁN HỌC 10 CÙNG STRONG TEAM
- › BẤT ĐẲNG THỨC COSI
- › HỆ THỨC LƯỢNG TRONG TAM GIÁC
- › BÀI TẬP TRẮC NGHIỆM VÀ TỰ LUẬN ÔN THI HỌC KÌ 1 MÔN TOÁN LỚP 10 (CÓ ĐÁP ÁN)
- › TÓM TẮT LÍ THUYẾT VÀ BÀI TẬP TRẮC NGHIỆM PHẦN MỆNH ĐỀ - TOÁN LỚP 10 CÓ ĐÁP ÁN
- › ÔN TẬP HỌC KÌ 2 MÔN TOÁN LỚP 10 THEO CHUYÊN ĐỀ
- › ĐỀ CƯƠNG ÔN TẬP MÔN TOÁN LỚP 10 - HỌC KÌ 2
- › BÀI TẬP TRẮC NGHIỆM CHƯƠNG 3 - ĐẠI SỐ 10
- › BÀI TẬP TRẮC NGHIỆM PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH TOÁN LỚP 10
- › TÓM TẮT LÍ THUYẾT VÀ BÀI TẬP PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
Bình luận (0)
- Trang chủ
- » TÀI LIỆU
- » Môn Toán
- » Toán lớp 10
TIN TỨC MỚI NHẤT
THỐNG KÊ LƯỢT XEM
Tổng truy cập 17,835,940
Đang online0
Tìm kiếm
ThS NGÔ VĂN DŨNG

FANPAGE
TƯ VẤN DU HỌC NTIC
- Mong muốn của chúng tôi là đồng hành cùng các bạn không chỉ tới lúc lên máy bay mà còn trợ giúp các bạn cho đến khi ra trường, làm việc và định cư tại đó.
- Nguyện vọng của chúng tôi là tất cả vì sự phát triển của con em chúng ta,
Rất mong được phục vụ quí vị.
Thông tin - chính sách
Liên hệ
ĐÀO TẠO TƯ VẤN DU HỌC NTIC
Địa chỉ: Đường nguyễn lương bằng, P.Hoà Khánh Bắc, Q.Liêu Chiểu, Tp.Đà Nẵng
Hotline: 0905540067 - 0778494857
Email: daotaontic@gmail.com
© Bản quyền thuộc về daykemtainha.info
- Powered by IM Group








Gửi bình luận của bạn