TÍNH CHẲN LẺ CỦA HÀM SỐ
Trung tâm luyện thi, gia sư - dạy kèm tại nhà NTIC Đà Nẵng giới thiệu phần TÍNH CHẲN LẺ CỦA HÀM SỐ nhằm hổ trợ cho các bạn có thêm tư liệu học tập. Chúc các bạn học tốt môn học này.
Ngày đăng: 17-10-2018
2,424 lượt xem

Định nghĩa :
Hàm số y = f(x) với tập xác định D gọi là hàm số chẵn nếu :
x ∈ D thì -x ∈ D và f(-x) = f(x).
lưu ý : đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
Hàm số y = f(x) với tập xác định D gọi là hàm số lẻ nếu :
x ∈ D thì -x ∈ D và f(-x) = -f(x).
lưu ý : đồ thị của hàm số lẻ nhận góc tọa độ làm tâm đối xứng.
+ D là tập đối xứng có dạng : [-a; a] với a ∈ R.
————————–
Phương pháp :
Bước 1 : tìm TXĐ : D chứng minh D là tập đối xứng.
Bước 2 : lấy x ∈ D => – x ∈ D.
Bước 3 : xét : f(-x) :
- Nếu f(-x) = … = f(x) : hàm số chẵn.
- Nếu f(-x) = … = – f(x) : hàm số lẻ.
- Nếu f(-x) = … ≠ – f(x) hoặc f(x): hàm số không chẵn, lẻ.
—————————-
Bài tập 1 : Xét tính chẵn lẻ của hàm số : y = f(x) = x3 + x
TXĐ : D = R
=> D là tập đối xứng.
lấy x ∈ D => – x ∈ D.
Xét f(-x) = (-x)3 + (-x) = -( x3 + x)= -f(x)
=> f(-x) = – f(x)
vậy : hàm số y = x3 + x là hàm số lẻ.
Bài tập 2 : Xét tính chẵn lẻ của hàm số : y = f(x) = x4 + x2 – 2
TXĐ : D = R
=> D là tập đối xứng.
lấy x ∈ D => – x ∈ D.
Xét : f(-x) = (-x)4 + (-x)2 – 2 = x4 + x2 – 2 = f(x)
=> f(-x) = f(x)
Vậy : hàm số y = x4 + x2 – 2 là hàm số chẵn.
Bài tập 3 : Xét tính chẵn lẻ của hàm số : y = f(x) = – 5
TXĐ : 2x + 8 ≥ 0 <=> x ≥ – 4
D = [-4; + ∞)
ta có : 5 ∈ D mà – 5 ∉ D => D không là tập đối xứng.
vậy : hàm số không chẵn, không lẻ.
Bài tập rèn luyện : Xét tính chẵn – lẻ của các hàm số sau :
LIÊN HỆ NGAY VỚI CHÚNG TÔI ĐỂ BIẾT THÊM THÔNG TIN CHI TIẾT
ĐÀO TẠO NTIC
Địa chỉ: Đường nguyễn lương bằng, P.Hoà Khánh Bắc, Q.Liêu Chiểu, Tp.Đà Nẵng
Hotline: 0905540067 - 0778494857
Email: daotaontic@gmail.com
Tin liên quan
- › ĐỀ THAM KHẢO MÔN TOÁN GIỮA KÌ 2 LỚP 12 THEO BẢN ĐẶC TẢ VÀ MA TRẬN
- › HƯỚNG DẪN GIẢI TOAN 12 - ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG
- › ĐỀ THI HỌC KÌ 1 - LỚP 12 MÔN TOÁN TẠI ĐÀ NẴNG NĂM HỌC 2019 - 2020
- › 8 CHỦ ĐỀ MÔN TOÁN ÔN THI THPT QUỐC GIA
- › PHƯƠNG PHÁP GIẢI BÀI TẬP TÍCH PHÂN
- › CÔNG THỨC TÍNH NHANH MÔN TOÁN 12
- › CÔNG THỨC TÍNH NHANH VỀ HÌNH CHÓP, HÌNH CẦU, HÌNH NÓN VÀ HÌNH TRỤ
- › LÍ THUYẾT VỀ LÃI ĐƠN LÃI KÉP VÀ BÀI TẬP VẬN DỤNG - ÔN THI THPT QUỐC GIA
- › BÀI TẬP TRẮC NGHIỆM - CÓ ĐÁP ÁN CHUYÊN ĐỀ MŨ VÀ LOGARIT - TÀI LIỆU ÔN THI THPT QUỐC GIA
- › 453 BÀI TẬP TRẮC NGHIỆM MÔN TOÁN - ÔN THI THPT QUỐC GIA - CÓ ĐÁP ÁN
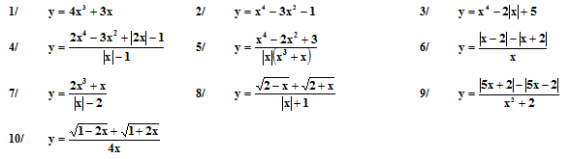









Gửi bình luận của bạn